The Weighted Perplexity Benchmark: Tokenizer-Normalized Evaluation for Language Model Comparison

Published: 7/7/2025

Abstract

Perplexity remains the primary intrinsic metric for evaluating language models, yet direct comparison across models with different tokenization schemes presents methodological challenges. We introduce a tokenizer-normalized perplexity metric that enables consistent comparison of language models regardless of their tokenization approaches. Through empirical analysis of 19 language models across five families on WikiText-2, we demonstrate how tokenization differences can affect traditional perplexity measurements by up to 21.6%. Our normalization method reveals the magnitude of tokenization effects on model comparisons and enables analysis of architectural efficiency patterns. We identify Llama Scout as performing substantially worse than models with far fewer active parameters. The Weighted Perplexity Benchmark provides researchers with a principled approach to evaluate language models while controlling for tokenization strategies.

Authors: Jessica Taylor, Vie McCoy

1. Introduction

As language model architectures, training approaches, and tokenization strategies diversify, comparing their fundamental text prediction capabilities has become increasingly difficult. Perplexity, defined as the exponentiated average negative log-likelihood of a sequence, remains the standard intrinsic evaluation metric. However, different tokenization schemes create systematic differences in perplexity comparisons that complicate cross-model evaluation.

This post addresses the need for tokenizer-independent evaluation metrics through the Weighted Perplexity Benchmark (WPB). Our contributions include:

1. A mathematical framework for normalizing perplexity scores across different tokenization schemes
2. Empirical evaluation of 19 language models demonstrating significant tokenization effects
3. Analysis of how tokenization differences affect model comparisons
4. Identification of architectural efficiency patterns when tokenization effects are controlled

2. Background and Related Work

2.1 Perplexity and Tokenization Dependencies

For a tokenized sequence $X = (x_1, x_2, \ldots, x_t)$ and model $M$, perplexity is defined as:

$\text{PPL}_M(X) = \exp\left(-\frac{1}{t}\sum_{i=1}^{t} \ln p_M(x_i|x_{<i})\right)$

The critical issue is that $t$ (the number of tokens) varies significantly across tokenizers for identical text. As noted by Mielke et al. (2019), this creates systematic differences in perplexity scores that complicate fair comparison.

2.2 Prior Normalization Approaches

Several approaches have been proposed to address tokenization differences in language model evaluation:

Bits-per-character (BPC): Widely used in character-level language modeling, BPC measures the average number of bits needed to encode each character (Graves, 2013). As shown by Bauwens (2024), BPC can be derived from token-level perplexity through normalization by character count.

Per-byte perplexity: The llama.cpp project has explored normalizing perplexity by the number of bytes in the original text rather than tokens, enabling comparison across models with different vocabulary sizes.

Character-level evaluation: Direct evaluation at the character level avoids tokenization differences entirely but requires models specifically designed for character-level prediction (Mielke et al., 2019).

Marginal tokenization: Cao & Rimell (2021) propose marginalizing over possible tokenizations, though this requires significant computational overhead, and implementation is more complex.

Some of these approaches would require changes to LLM inference toolchains. Our work provides a simple normalization that can be applied to any token-level language model. In particular, we used llama.cpp for perplexity evaluation, and then adjusted from there.

3. Methodology

3.1 Tokenizer-Normalized Perplexity

We introduce a normalization that adjusts perplexity scores to a common tokenization baseline. Given two models $A$ and $B$ with tokenizers producing $n_A$ and $n_B$ tokens respectively for the same text:

The total negative log-likelihood for model $B$ is:

$\text{Total NLL}_B = n_B \times \ln(\text{PPL}_B)$

The normalized perplexity of model $B$ relative to model $A$'s tokenization is:

$\text{Normalized PPL}_B = \exp\left(\frac{\text{Total NLL}_B}{n_A}\right) = \text{PPL}_B^{(n_B/n_A)}$

This adjustment redistributes the total prediction loss across the reference number of tokens. When $n_B > n_A$, model $B$ makes more predictions for the same text, and its perplexity is adjusted upward. When $n_B < n_A$, the adjustment is downward.

As a quick check, consider a hypothetical LLM that predicted text equally well to Llama 70B, but whose tokenizer produced twice as many tokens. We would expect its total NNL to equal Llama 70B’s total NNL. Let model A be Llama 70B, and model B be this different model. We can write:

$n_A \times \ln(\text{PPL}_A) = \text{Total NLL}_A = \text{Total NLL}_B = 2 n_A \times \ln(\text{PPL}_B)$

$\ln(\text{PPL}_A) = 2 \ln(\text{PPL}_B)$

$\text{PPL}_A = \text{PPL}_B^2$

$\text{Normalized PPL}_B = \text{PPL}_B^2 = \text{PPL}_A = \text{Normalized PPL}_A$

This quick check confirms that our formula for normalized PPL evaluates the two models equally, despite tokenization differences.

Method assumptions: This approach assumes that the total information content of the text remains constant across tokenizations, redistributing the prediction difficulty across fewer or more tokens. While tokenization schemes may create systematically easier or harder prediction tasks, this provides a principled baseline for comparison.

3.2 Evaluation Protocol

We tested a number of base models on WikiText-2, using llama.cpp and FP8 quantization, on a Mac Studio (512GB unified memory). We got gguf quantized models from mradermacher on Hugging Face, and/or the GGUF My Repo llama.cpp based tool, also on Hugging Face.

We evaluated 18 models across five families on WikiText-2: Llama (5 models), Gemma (4 models), Qwen (6 models), Mixtral (2 models), and DeepSeek (1 model). Models range from 0.5B to 236B parameters and include both dense and Mixture-of-Experts architectures. We use Llama 3's tokenizer as the reference baseline, chosen for its temporal priority and widespread adoption.

4. Results

4.1 Empirical Tokenization Differences

Our analysis of WikiText-2 across major model families reveals substantial tokenization variations:

Family	Token Count	% Difference from Llama
Llama 3	288,768	0% (reference)
Llama 4	288,252	-0.2%
Gemma	294,912	+2.1%
DeepSeek	305,152	+5.7%
Qwen	299,008	+3.5%
Mixtral	328,704	+13.8%

These differences directly impact perplexity calculations, making cross-family comparisons challenging to interpret without normalization.

4.2 Tokenization Impact on Model Comparisons

This table shows original versus normalized perplexity scores:

Model	PPL	Tokens	Normalized PPL	Change
Llama 3.2 1B	10.195	288,768	10.195	0
Llama 3.2 3B	8.082	288,768	8.082	0
Llama 3.1 8B	6.404	288,768	6.404	0
Llama 3.1 70B	2.824	288,768	2.824	0
Llama 4 Scout	8.840	288,252	8.805	–0.39%
Gemma 3 1B	10.801	294,912	11.362	+5.19%
Gemma 3 4B	7.438	294,912	7.762	+4.36%
Gemma 3 12B	5.776	294,912	5.996	+3.80%
Gemma 3 27B	4.740	294,912	4.899	+3.37%
Qwen 2.5 0.5B	13.908	299,008	15.269	+9.78%
Qwen 2.5 1.5B	9.802	299,008	10.628	+8.43%
Qwen 2.5 3B	8.424	299,008	9.085	+7.85%
Qwen 3 4B	8.151	299,008	8.780	+7.72%
Qwen 3 8B	7.224	299,008	7.749	+7.26%
Qwen 3 30B-A3B	6.256	299,008	6.676	+6.72%
Mixtral 8×7B	4.104	328,704	4.989	+21.56%
Mixtral 8×22B	2.973	328,704	3.457	+16.26%
DeepSeek V2	3.980	305,152	4.304	+8.15%

Key findings:

1. Mixtral models experience the largest adjustment (up to 21.6% increase in perplexity), corresponding to their 13.8% higher token count.
2. Magnitude of tokenization effects: Changes range from 0% (reference family) to over 20%.
3. Systematic patterns: Models using tokenizers that segment text more finely have lower raw perplexity scores, as expected from the mathematical relationship between token count and per-token prediction difficulty.

4.3 Architectural Analysis

The normalization enables analysis of architectural efficiency patterns:

Dense Model Scaling: Among dense models, we expect a relationship between parameter count and normalized perplexity. This plot shows parameters versus normalized PPL, for the 13 dense models:

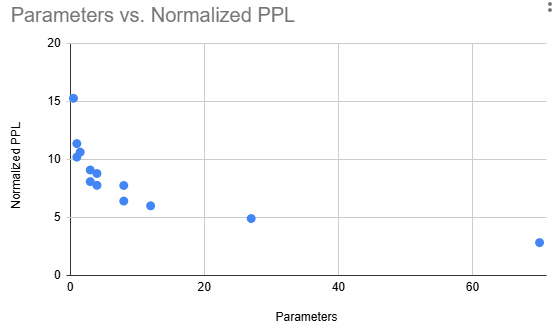
To fit a curve, we take the natural log of both parameter count and normalized PPL, and then apply linear regression:

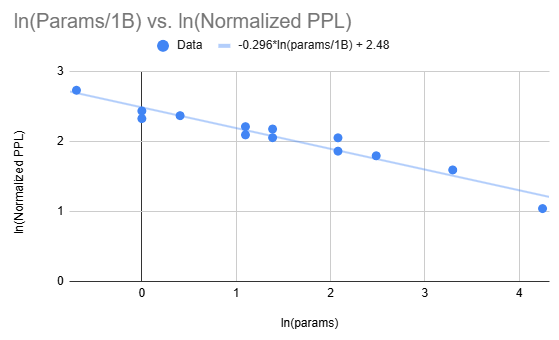
Our approximation is

$\ln\left(\text{Normalized PPL}\right) \approx -0.296 \cdot \ln\left(\frac{\text{Params}}{1B}\right) + 2.48$

We have $R^2 = 0.943$, showing a reasonably strong fit. To put this in perspective, a doubling of parameter count reduces normalized PPL by about 18.5%, and a 10x in parameter count reduces normalized PPL by about 49.4%. Or to be more succinct: 10x in parameters means approximately a halving of normalized perplexity.

The limited number of models and variation across model families constrains statistical confidence in these relationships.

Mixture-of-Experts Performance: Mixtral models maintain competitive performance after normalization. However, architectural conclusions should be drawn cautiously given the limited sample size.

4.4 Llama Scout: An Architectural Outlier

Llama Scout emerges as a striking outlier in our analysis. Despite approximately 17B active parameters per forward pass (from ~109B total parameters), it achieves normalized perplexity of 8.81—worse than Llama 3.2 3B (8.08) which has 5.7× fewer active parameters. This suggests significant inefficiencies in this particular Mixture-of-Experts implementation, though generalizations about MoE architectures should be made cautiously based on a single example.

To check if quantization was affecting performance, we tested a FP16 version of Llama Scout, yielding a (un-normalized) PPL of 8.8486, hardly different from the PPL of the FP8 version, 8.8396. Hence, FP8 quantization does not explain Llama Scout’s poor performance.

4.5 Implications for Model Evaluation

Our results demonstrate that tokenization differences substantially affect model comparisons:

1. Magnitude of effects: Up to 21.6% difference in apparent performance associated with tokenization differences
2. Evaluation consistency: Normalization provides more consistent comparison baselines across model families
3. Architectural insights: Controlling for tokenization enables cleaner analysis of design trade-offs

5. Discussion

5.1 Methodological Implications

The Weighted Perplexity Benchmark addresses tokenization inconsistencies in current evaluation practice. The framework enables:

1. Consistent cross-family comparison of language models
2. Controlled assessment of architectural innovations
3. Cleaner analysis of scaling relationships

5.2 Relationship to Prior Work

Our approach builds on established normalization concepts from BPC and character-level evaluation but applies them in a computationally simple way to existing token-level models. This approach works easily with existing toolchains such as llama.cpp.

5.3 Limitations and Future Work

Several limitations constrain our analysis:

1. Single dataset: Results are demonstrated only on WikiText-2; generalization across domains and languages requires validation. Particular benchmarks, especially ones with public data, can be gamed over time.
2. Statistical validation: A limited set of tested models limits statistical confidence.
3. Limited architectural diversity: Conclusions about MoE efficiency rest on limited examples.

Future work should extend validation to multiple datasets and languages, and test a broader set of models. Additionally, the method should be validated by independent implementations. The relevance of perplexity can also be assessed generally by finding its relationship with other benchmarks.

6. Conclusion

We have introduced the Weighted Perplexity Benchmark, a tokenizer-normalized evaluation framework that enables more consistent comparison of language models across different tokenization schemes. Our analysis of 19 models reveals substantial effects of tokenization differences on perplexity evaluations, with changes of up to 21.6%.

The framework provides researchers with a principled approach to language model evaluation that controls for tokenization differences, while working with existing toolchains such as llama.cpp. This enables more consistent assessment of architectural innovations and cleaner analysis of scaling behaviors. The method is simple to implement and can be applied to any tokenized evaluation dataset.

Our findings highlight the importance of methodological rigor in language model evaluation. While this approach addresses tokenization inconsistencies, broader validation across datasets, reference choices, and evaluation metrics will strengthen its applicability to the field.

References

Bauwens, T. (2024). Bits-per-character and its relation to perplexity. Personal Blog. https://bauwenst.github.io/posts/explainers/2024-07-29-Bits-per-character/

Cao, S., & Rimell, L. (2021). You should evaluate your language model on marginal likelihood over tokenisations. ACL.

Graves, A. (2013). Generating sequences with recurrent neural networks. arXiv:1308.0850.

Mielke, S. J., Cotterell, R., Gorman, K., Roark, B., & Eisner, J. (2019). What kind of language is hard to language-model? ACL.